
- Зохиолч Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Хамгийн сүүлд өөрчлөгдсөн 2025-01-22 17:05.
Эхний захиалга дифференциал тэгшитгэл байна яг хэрэв энэ нь хадгалагдсан хэмжигдэхүүнтэй бол. Жишээлбэл, салгаж болох тэгшитгэлүүд үргэлж байдаг яг , учир нь тодорхойлолтоор тэдгээр нь: M(y)y + N(t)=0 хэлбэртэй тул ϕ(t, y) = A(y) + B(t) нь хадгалагдсан хэмжигдэхүүн юм.
Цаашилбал, дифференциал тэгшитгэлийг салгах боломжтой юу?
Салгаж болох тэгшитгэлүүд . Анхны захиалга дифференциал тэгшитгэл y'=f(x, y)-г a гэж нэрлэдэг салгаж болох тэгшитгэл хэрэв f(x, y) функцийг x ба y-ийн хоёр функцийн үржвэрт оруулж чадвал: f(x, y)=p(x)h(y), энд p(x) ба h(y) нь тасралтгүй функцууд.
Мөн dy dx xy-г хэрхэн нэгтгэх вэ? Алхам 1 Бүх у гишүүнийг тэгшитгэлийн нэг тал руу, бүх x гишүүнийг нөгөө тал руу шилжүүлж хувьсагчдыг салга.
- Хоёр талыг dx:dy = (1/y) dx-ээр үржүүлнэ. Хоёр талыг y-ээр үржүүлнэ: y dy = dx.
- Интеграл тэмдгийг урд нь тавина:∫ y dy = ∫ dx. Тал бүрийг нэгтгэх: (y2)/2 = x + C.
- Хоёр талыг 2-оор үржүүлнэ: y2 = 2(x + C)
Ийм байдлаар дифференциал тэгшитгэл яг хэзээ вэ?
Өгөгдсөн тэгшитгэл яг байна учир нь хэсэгчилсэн деривативууд нь адилхан: ∂Q∂x=∂∂x(x2+3y2)=2x, ∂P∂y=∂∂y(2xy)=2x.
dy dx гэж юу гэсэн үг вэ?
d/dx-ээр бид ялгах функц байгаа гэсэн үг; Аливаа зүйлийн d/dx гэдэг нь "ямар нэгэн зүйл"-ийг x-тэй харьцуулан ялгах ёстой гэсэн үг юм. dy/dx гэж "х-тэй холбоотойгоор y-г ялгах" гэсэн утгатай dy/dx d/dx(y)-тай ижил утгатай.
Зөвлөмж болгож буй:
Робинсоны проекцын зураг үнэн зөв үү?
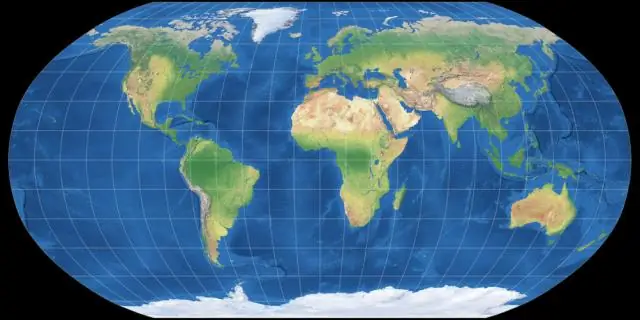
Робинсоны төсөөлөл нь азимутал биш юм; бүх чиглэлийг үнэн зөв харуулсан ямар ч цэг эсвэл цэг байхгүй. Робинсоны төсөөлөл нь өвөрмөц юм. Үүний гол зорилго нь дэлхий даяар харагдахуйц сонирхолтой газрын зургийг бүтээх явдал юм
Дэлхийн газрын зураг үнэн зөв үү?

Дэлхийн ихэнх газрын зураг бүрэн үнэн зөв биш гэдгийг бид бүгд мэднэ. Ангийн хана болон атлас дээр наасан байгаа газрын зургийг Меркаторын проекц гэж нэрлэдэг бөгөөд анх 1569 онд Фламандын газарзүйч Герардус Меркатор танилцуулсан байдаг
ДНХ-ийн хуулбар үнэн зөв байх нь яагаад чухал вэ?

Эс хуваагдахаас өмнө охин эс бүр генетикийн мэдээллийг бүрэн, зөв хүлээн авахын тулд ДНХ-ээ үнэн зөв хуулбарлах ёстой. ДНХ-ийн репликаци нь үнэн зөвийг баталгаажуулахад тусалдаг засварын процессыг агуулдаг
Weight Watchers дижитал жинлүүр үнэн зөв үү?

Weight Watchers жинлүүр нь өндөр тодосгогчтой, уншихад хялбар 1.3”-1.9” дэлгэцтэй. Та үнэхээр ямар жинтэй болохыг мэдмээр байна уу? Энэ бол гэрийн жингийн зах зээл дээрх хамгийн нарийвчлалтай жинлэх технологи бөгөөд цаг хугацааны хувьд хамгийн нарийвчлалтай юм
Элементийг физик аргаар салгаж болох уу?

Гетероген хольц гэдэг нь хоёр ба түүнээс дээш химийн бодис (элемент эсвэл нэгдлүүд) -ийн холимог бөгөөд янз бүрийн бүрэлдэхүүн хэсгүүдийг нүдээр ялгаж, физик аргаар хялбархан салгаж болно. Жишээ нь: элс, усны холимог
