
Агуулгын хүснэгт:
- Зохиолч Miles Stephen stephen@answers-science.com.
- Public 2024-01-18 08:17.
- Хамгийн сүүлд өөрчлөгдсөн 2025-01-22 17:05.
Хязгааргүй олонлогийн жишээ:
- Тохируулах Хавтгайн бүх цэгийн хязгааргүй олонлог .
- Тохируулах Шугамын сегментийн бүх цэгийн хязгааргүй олонлог .
- Тохируулах бүх эерэг бүхэл тоонуудын 3-ын үржвэр нь a хязгааргүй олонлог .
- W = {0, 1, 2, 3, ……..} i.e. тогтоосон бүх бүхэл тоонуудын нэг хязгааргүй олонлог .
- N = {1, 2, 3, ……….}
- Z = {………
Үүний нэгэн адил та хязгааргүй олонлогийг хэрхэн харуулах вэ гэж асууж магадгүй юм.
Хоёр зүйлийг үзүүлснээр олонлог хязгааргүй гэдгийг баталж чадна
- Өгөгдсөн n-ийн хувьд n урттай дор хаяж нэг элементтэй байна.
- Хэрэв энэ нь хамгийн дээд хязгаарлагдмал урттай элементтэй бол та илүү урт элементийг барьж болно (ингэснээр энэ нь хамгийн дээд хязгаарлагдмал урттай элементийг үгүйсгэнэ).
Хоёрдугаарт, олонлог хязгааргүй эсвэл төгсгөлтэй эсэхийг яаж тодорхойлох вэ? Олонлогийг төгсгөлтэй эсвэл хязгааргүй гэж тодорхойлох цэгүүд нь:
- Хэрэв олонлог нь эхлэл ба төгсгөлийн цэгтэй бол энэ нь төгсгөлтэй, харин эхлэх эсвэл төгсгөлгүй бол хязгааргүй олонлог болно.
- Хэрэв олонлог хязгаарлагдмал тооны элементтэй бол энэ нь төгсгөлтэй, харин түүний элементийн тоо хязгааргүй бол хязгааргүй болно.
Хоёрдугаарт, жишээгээр хязгаарлагдмал ба хязгааргүй багц гэж юу вэ?
Жишээ -ийн Хязгааргүй багц Хэрвээ тогтоосон а биш хязгаарлагдмал олонлог , тэгвэл энэ нь a хязгааргүй олонлог . Натурал тоо ба бүхэл тоо хоёр байна жишээнүүд -ийн багц тэр нь хязгааргүй тиймээс тийм биш хязгаарлагдмал . Том үсгээр том үсгээр тэмдэглэсэн Z үсгийг ихэвчлэн заадаг тогтоосон бүхэл тоонуудын.
Хязгааргүй олонлог байдаг уу?
Ямар ч байхгүй хязгааргүй олонлогууд . Ганц тийм биш хязгааргүй олонлог хийх үгүй байдаг , гэхдээ энэ үзэл баримтлал нь логикийн хувьд зөрчилддөг - "дөрвөлжин тойрог" -оос ялгаагүй. Хязгааргүй олонлогууд Эдгээр нь математикийн орчин үеийн үндэс суурьт шууд утгаараа тусгагдсан байдаг бөгөөд үүнийг “The аксиом” гэж нэрлэдэг. Хязгааргүй байдал ”.
Зөвлөмж болгож буй:
Олон атомт ион агуулсан нэгдлүүдийн томъёог хэрхэн бичих вэ?
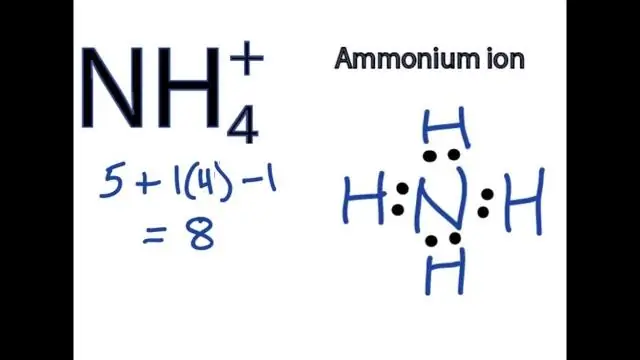
Олон атомт ион агуулсан нэгдлүүдийн томьёо бичихдээ металлын ионы тэмдэг, дараа нь олон атомт ионы томъёог бичиж, цэнэгийг тэнцвэржүүлнэ. Олон атомт ион агуулсан нэгдлүүдийг нэрлэхийн тулд эхлээд катион, дараа нь анионыг хэлнэ үү
Та Mac дээр A тэнцүү биш тэмдгийг хэрхэн бичих вэ?

Математик Mac гар дээрх тэнцүү биш тэмдгийг үүсгэхийн тулд "Тэгш" гэсэн товчлол юм. Өөр нэг хэрэгтэй гарын хослол бол Option ShiftEquals бөгөөд энэ нь нэмэх эсвэл хасах тэмдгийг үүсгэдэг
Та PbO хэрхэн бичих вэ?

PbO, Хар тугалга (II) оксидын нэрийг хэрхэн бичих тухай тайлбар. Эхлээд бид PbO нь ион эсвэл молекул (ковалентын) нэгдэл эсэхийг үечилсэн систем ашиглан тодорхойлно. Үелэх системээс Pb нь металл, О нь металл бус юм. Тиймээс PbO нь метал ба металл бус хоёроос бүрддэг тул ионы нэгдэл юм
Хоёр цэг өгсөн тэгшитгэлийг цэгийн налуу хэлбэрээр хэрхэн бичих вэ?

Шугамын тэгшитгэлийг бичиж болох янз бүрийн хэлбэрүүд байдаг: цэгийн налуу хэлбэр, налуу огтлолцлын хэлбэр, стандарт хэлбэр гэх мэт. Шугамын тэгшитгэлд хоёр цэг (x1, y1) ба (x2, y2) өгөгдсөн. ) шугам өнгөрөхийг, ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))-аар өгнө
Хязгааргүй хязгаар ба хязгааргүй хязгаар хоёрын ялгаа юу вэ?

Хязгааргүй хязгаартай харьцах үед энэ нь босоо асимптот болохыг анхаарна уу. Хязгааргүй байдлын хязгаарууд нь бас асимптотууд боловч эдгээр нь бидний энэ удаад тулгарч буй хэвтээ асимптотууд юм. Хязгааргүй хязгаарт "х хязгаар нь хязгааргүйд ойртох үед эсвэл сөрөг хязгааргүй" гэсэн тэмдэглэгээнд байгаа асуудал гардаг
