
- Зохиолч Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Хамгийн сүүлд өөрчлөгдсөн 2025-01-22 17:05.
Тиймээс a-тай экспоненциал функц сөрөг суурь , гэх мэт тийм ч их функц биш (энэ нь тасралтгүй биш), оноос хойш чадна зөвхөн байх маш тодорхой х-утгуудаар үнэлэгддэг. Ийм шалтгааны улмаас бид зөвхөн эерэг логарифмуудыг авч үздэг суурь , зэрэг сөрөг суурь тасралтгүй биш, ерөнхийдөө ашиггүй.
Үүнтэй холбогдуулан лог яагаад сөрөг суурьтай байж болох вэ?
Тиймээс 0, 1, бүр сөрөг тоо нь болзошгүй асуудал үүсгэдэг суурь хүч чадлын функц. Хэрэв эдгээр тоонууд байвал чадна найдвартай биш байх нь суурь чадлын функцийн хувьд тэд мөн чадна найдвартай биш байх нь суурь -ийн а логарифм . Ийм учраас бид 1-ээс бусад эерэг тоог л зөвшөөрнө суурь -ийн логарифм.
Дээрхээс гадна сөрөг бүртгэл гэж юу гэсэн үг вэ? А сөрөг логарифм гэсэн үг тоогоор хэдэн удаа хуваах вэ.
Үүний нэгэн адил логны суурь сөрөг тоо байж болох уу гэж асуудаг.
оноос хойш суурь b эерэг (b>0), the суурь b y-ийн зэрэглэлд хүрсэн нь эерэг байх ёстой (by>0) ямар ч бодит y. Тиймээс тоо x эерэг байх ёстой (x>0). Жинхэнэ суурь б логарифм -ийн а сөрөг тоо тодорхойгүй байна.
0-ийн лог хэд вэ?
бүртгэл 0 тодорхойгүй байна. Үр дүн нь бодит тоо биш юм, учир нь та ямар ч зүйлийг өөр ямар ч хүчин зүйлээр өсгөх замаар хэзээ ч тэг авч чадахгүй. Та тэг рүү хэзээ ч хүрч чадахгүй, зөвхөн хязгааргүй их, сөрөг хүчийг ашиглан түүнд ойртож чадна. Бодит логарифм функц logb(x) нь зөвхөн x>-д тодорхойлогддог 0.
Зөвлөмж болгож буй:
Чи квадрат сөрөг байж болох уу?
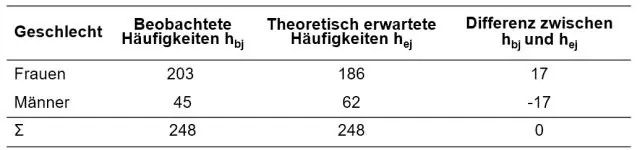
Чи: Чи квадратын утга сөрөг байж болох уу? Хариулт нь үгүй. Хи квадратын утга нь сөрөг байж болохгүй, учир нь энэ нь квадратын зөрүүний нийлбэр (олж авсан болон хүлээгдэж буй үр дүнгийн хооронд) дээр суурилдаг
Сөрөг ба эерэг налуу параллель байж болох уу?

Теорем 104: Хэрэв хоёр шулуун ижил налуутай бол тэдгээр нь босоо бус параллель шулуун байна. Хэрэв хоёр шулуун перпендикуляр бөгөөд аль нь ч босоо биш бол тэдгээрийн аль нэг нь эерэг налуутай, нөгөө нь сөрөг налуутай байна. Мөн тэдгээрийн налуугийн үнэмлэхүй утгууд нь харилцан хамааралтай байдаг
Уян хатан потенциал энерги сөрөг байж болох уу?

Та рашаан дээр ажил хийж, өөрөөр хэлбэл түүнд энерги шилжүүлж байгаа тул түүнд хуримтлагдсан боломжит энергийг нэмэгдүүлж байна. Боломжит энерги нь хэзээ ч сөрөг байж болохгүй x=0 үед PE тэг байна гэсэн үндэслэлтэй тодорхойлолтыг хийх
Арифметик цувралын нийлбэр сөрөг байж болох уу?

Арифметик дарааллын зан байдал нь нийтлэг ялгаанаас хамаарна d. Хэрэв нийтлэг ялгаа d нь: Эерэг байвал дараалал нь хязгааргүй (+∞) Сөрөг, дараалал нь сөрөг хязгаар (&хасах;∞) руу регресс болно
50 суурь хос хос судалтай ДНХ 100 суурь нь 25 аденины суурьтай бол нийт хэдэн гуанины суурьтай байх вэ?

Тэгэхээр нийт 25+25=50 аденин ба тимин суурь байна. 100-50=50 суурь үлдэнэ. Цитозин ба гуанин нь хоорондоо холбогддог тул тэдгээрийн хэмжээ тэнцүү байдаг гэдгийг анхаарна уу. Одоо бид гуанин эсвэл цитозины суурийн тоог 2-т хувааж болно
