
- Зохиолч Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Хамгийн сүүлд өөрчлөгдсөн 2025-06-01 05:05.
Зүгээр л 2х2 гэж бод матриц тэр бол түүний урвуутай төстэй диагональ оруулгууд нь 1 эсвэл -1 байхгүйгээр. Диагональ матрицууд заавал тэгнэ ээ. Тиймээс, А ба урвуу А нь төстэй , тиймээс тэдний хувийн утга ижил байна. хэрэв А-ийн хувийн утгуудын аль нэг нь n бол хувийн утга түүний урвуу 1/n байх болно.
Мөн матриц нь түүний шилжүүлэгтэй төстэй юу?
Ямар ч дөрвөлжин матриц талбай дээгүүр байна түүний шилжүүлэн суулгахтай төстэй болон аливаа дөрвөлжин цогцолбор матриц байна төстэй тэгш хэмт цогцолбор руу матриц.
Үүний нэгэн адил бүх урвуу матрицууд ижил төстэй юу? Хэрэв А ба В бол төстэй болон урвуу , дараа нь A-1 ба B-1 байна төстэй . Баталгаа. Түүнээс хойш бүгд нь матрицууд байна урвуу , бид хоёр талын урвуу талыг авч болно: B-1 = (P-1AP)-1 = P-1A-1(P-1)-1 = P-1A-1P, тиймээс A-1 ба B-1 нь төстэй . Хэрэв А ба В бол төстэй , аль ч k = 1, 2, -ийн хувьд Ak ба Bk нь мөн адил байна.
Үүнтэй холбогдуулан матриц өөртэйгөө төстэй байж болох уу?
Өөрөөр хэлбэл, Any матриц байна өөртэйгөө төстэй : I−1AI=A. Хэрэв А бол төстэй B хүртэл, тэгвэл B байна төстэй A-д: хэрэв B=P−1AP бол A=PBP−1=(P−1)−1BP−1. Хэрэв А бол төстэй B=P−1AP-ээр дамжуулан B руу, C нь байна төстэй C=Q−1BQ-ээр дамжуулан B руу, тэгвэл А байна төстэй C-д: C=Q−1P−1APQ=(PQ)−1APQ.
Хэрэв матрицууд ижил байвал юу гэсэн үг вэ?
Шугаман алгебрт хоёр n-н-ээр матрицууд A ба B гэж нэрлэдэг ижил төстэй бол урвуу n-by-n гэж байдаг матриц Ийм P. Үүнтэй төстэй матрицууд ижил шугаман зургийг хоёр (магадгүй) өөр суурийн дор төлөөлөх ба P нь суурийн өөрчлөлт юм матриц.
Зөвлөмж болгож буй:
Матриц гэдэг үг нь митохондритай ямар холбоотой вэ?
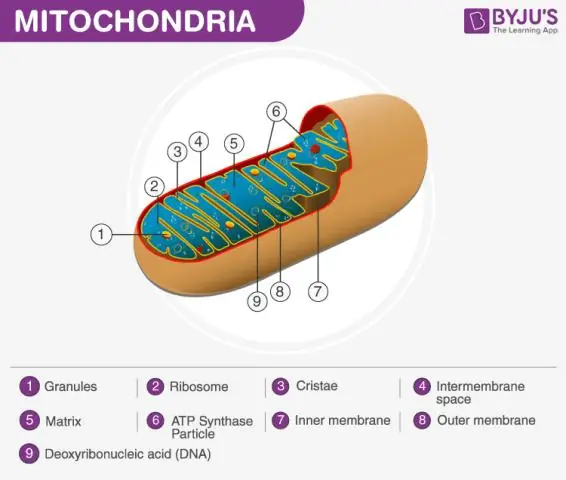
Митохондрийн матрицыг тодорхойлсон Митохондри нь гаднах мембран, дотоод мембран, матриц гэж нэрлэгддэг гель хэлбэртэй материалаас бүрдэнэ. Энэ матриц нь бага ус агуулдаг тул эсийн цитоплазмаас илүү наалдамхай байдаг. Энэ нь ATP хэмээх энергийн молекулуудыг үүсгэдэг эсийн амьсгалын чухал алхам юм
Матриц дахь вектор гэж юу вэ?
Скаляр, вектор ба матрицууд Скаляр гэдэг нь 3, -5, 0.368 гэх мэт тоо, Авектор нь тоонуудын жагсаалт (мөр, баганад байж болно), Аматрикс нь тоонуудын массив (нэг буюу хэд хэдэн мөр, нэг эсвэл) юм. илүү багана)
Дискрет математикийн матриц гэж юу вэ?
Дискрет математик ба түүний хэрэглээ Бүлэг 2 Тэмдэглэл 2.6 Матрицууд Лекцийн слайдууд by Adil Aslammailto:[email protected]. Матрицын тодорхойлолт •Матриц гэдэг нь тоонуудын тэгш өнцөгт массив юм. m мөр, n баганатай матрицыг m x n матриц гэнэ. Матрицын олон тоо нь матриц юм
Эсийн гаднах матриц юу хийдэг вэ?

Төрөл бүрийн шинж чанар, найрлагатай учраас ECM нь дэмжлэг үзүүлэх, эд эсийг бие биенээсээ тусгаарлах, эс хоорондын холбоог зохицуулах зэрэг олон үүргийг гүйцэтгэдэг. Эсийн гаднах матриц нь эсийн динамик зан үйлийг зохицуулдаг
Хажуу талын өнцгийн SAS ижил төстэй байдлын постулатыг ашиглан ижил төстэй 2 гурвалжинг хэрхэн батлах вэ?

SAS ижил төстэй байдлын теорем нь хэрэв нэг гурвалжны хоёр тал нь нөгөө гурвалжны хоёр талтай пропорциональ бөгөөд хоёуланд нь багтсан өнцөг нь тэнцүү бол хоёр гурвалжин ижил төстэй байна. Ижил төстэй байдлын хувиргалт нь нэг буюу хэд хэдэн хатуу хувирал, дараа нь өргөтгөл юм
