Агуулгын хүснэгт:
Видео: Дугуй диаграм дээрх секторын өнцгийг хэрхэн олох вэ?
2024 Зохиолч: Miles Stephen | [email protected]. Хамгийн сүүлд өөрчлөгдсөн: 2023-12-15 23:39
1 Хариулт
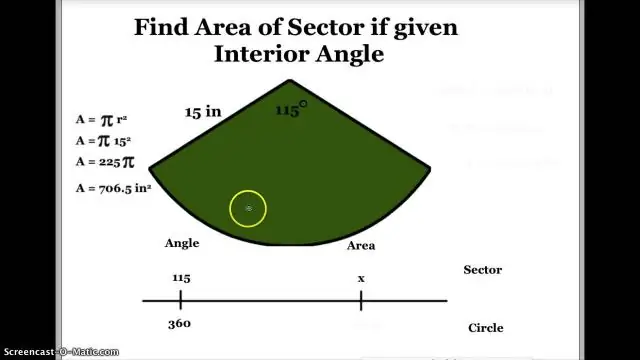
- Аль ч тохиолдолд салбар , анхаарах ёстой 3 хэсэг байна:
- Нумын урт нь тойргийн нэг хэсэг юм. The салбар талбай нь нийт талбайн нэг хэсэг юм. The салбарын өнцөг 360°-ийн бутархай юм
- Хэрэв салбар -ийн 20% байна дугуй диаграм , эдгээр хэсгүүдийн аль нэг нь нийт хэсгийн 20% байна.
- 20%×360°
- 20100×360=72°
Ийм байдлаар тойргийн секторын зэрэглэлийг хэрхэн олох вэ?
Тайлбар: Төвийн өнцгийг хэмжвэл60 градус , нийт 360-ыг хуваа градус дахь тойрог 60-аар. Үүнийг харгалзах нумын хэмжигдэхүүнээр үржүүл олох нийт тойрог тойрог . Тойрог ашиглана уу олох theradius, дараа нь радиусыг ашиглана олох газар.
Дараа нь асуулт бол дугуй диаграм дахь төв өнцөг гэж юу вэ? Дотор дугуй диаграм , төрөл бүрийн ажиглалт эсвэл бүрэлдэхүүн хэсгүүдийг тойргийн секторуудаар, бүхэл тойрог нь бүх бүрэлдэхүүн хэсгүүдийн утгын нийлбэрийг илэрхийлдэг. төв өнцөг бүрэлдэхүүн хэсгийн хувьд дараах байдлаар өгөгдсөн: Төвийн өнцөг бүрэлдэхүүн хэсгийн хувьд = Бүрэлдэхүүний утга Бүх бүрэлдэхүүн хэсгүүдийн утгын нийлбэр × 360°
Үүний нэгэн адил хувь хэмжээний зэрэглэлийг хэрхэн олох вэ?
Нэг тойрогт 360 байна градус , тиймээс хэрэв та өнцгийг a-ээр илэрхийлэхийг хүсвэл хувь , зүгээр л өнцгийн хэмжилтийг хуваана (д градус ) 360-аар үржүүлж, 100-аар үржүүлнэ. Эсрэгээр нь хуваана хувь 100-аар үржүүлж, 360-аар үржүүлнэ.
Төвийн өнцгийг олох томьёо юу вэ?
Томъёо for S=rθ Доорх зураг нь радиус ба тэдгээрийн хоорондын хамаарлыг харуулж байна төв өнцөг радианаар. The томъёо S=rθ энд s нь нумын уртыг, S=rθ -ийг илэрхийлнэ төв өнцөг радианаар ба r нь радиусын урт.
Зөвлөмж болгож буй:
Салбарын талбай ба радиусыг өгсөн төвийн өнцгийг хэрхэн олох вэ?
Секторын талбайгаас төв өнцгийг тодорхойлох (πr2) × (төв өнцөг ÷ 360 градусаар) = секторын талбай. Хэрэв төвийн өнцгийг радианаар хэмжвэл оронд нь томьёо нь: секторын талбай = r2 × (радианаар төв өнцөг ÷ 2) болно. (θ ÷ 360 градус) × πr2. (52.3 ÷ 100π) × 360. (52.3 ÷ 314) × 360
Хоёр талт трапецын суурийн өнцгийг хэрхэн олох вэ?
Изосцелестрепезидын суурь (дээд ба доод) параллель байна. Изосцелестрапезидын эсрэг талууд нь ижил урттай (конгруент). Суурийн хоёр талын өнцөг нь ижил хэмжээтэй/хэмжээтэй (тохирсон)
Тойргийн секторын уртыг хэрхэн олох вэ?
Том нумын дагуух төв өнцгийн хэмжээ нь 180°-аас их байна. Нумын уртын томьёог тойргийн нумын уртыг олоход ашигладаг; l=rθ l = r θ, хаана θ радианд байна. Салбарын талбай A=12θr2 A = 1 2 θ r 2, хаана θ радианд байна
Нумын урт ба секторын талбайг хэрхэн олох вэ?
Том нумын дагуух төв өнцгийн хэмжээ нь 180°-аас их байна. Нумын уртын томьёог тойргийн нумын уртыг олоход ашигладаг; l=rθ l = r θ, хаана θ радианд байна. Салбарын талбай A=12θr2 A = 1 2 θ r 2, хаана θ радианд байна
Та ээлжлэн ба харгалзах өнцгийг хэрхэн олох вэ?
Харгалзах өнцгүүдийн нэг нь үргэлж дотоод (зэрэгцээ шугамын хооронд), нөгөө нь гаднах (зэрэгцээ шугамын хоорондох талбайн гадна) байдаг. Хөндлөн огтлолцох үед өөр өөр зэрэгцээ шугамаар үүсгэгдсэн, хөндлөн огтлолын эсрэг талд байрлах хоёр хурц өнцөг a ба c'-ийг ээлжлэн гэж нэрлэдэг